Ch. 3: Map Processing
INTRODUCTION
This chapter and the next focus on key concepts and the preprocessing of your data. Preprocessing is an important but unheralded subject. It shapes the datasets you place in the GIS; it prepares them for analysis. This chapter looks at preprocessing the map or spatial component of your features. The next chapter focuses on preprocessing your feature’s attributes. These are the “housecleaning” tasks mentioned in the first two chapters.
This chapter begins with concepts that define the geographical referencing standards of the Earth. Topics include latitude and longitude, projections, coordinate systems, and datums. These concepts help you understand map preprocesses like changing projections, converting layers from vector to raster, and reclassifying or resampling layers. A large part of map preprocessing is to make your data usable by providing consistent projection parameters throughout all your data sets. The goal is to make your layers fit properly over each other.
EARTH
Latitude and Longitude
Any feature can be referenced by its latitude and longitude, which are angles measured in degrees from the Earth’s center to a point on the Earth’s surface (see Figure 3.1). Across the spherical Earth, latitude lines stretch horizontally from east to west (left image in Figure 3.2), and they are parallel to each other, hence their alternative name, parallels. Longitude lines, also called meridians, stand vertically and stretch from the North Pole to the South Pole (center image in Figure 3.2). Together these “north to south” and “east to west” lines meet at perpendicular angles to form a graticule, a grid that encompasses the Earth (right image in Figure 3.2).
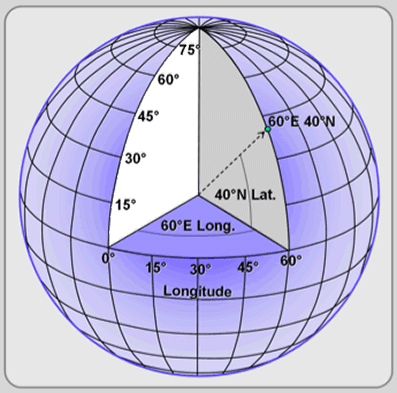
Figure 3.1: Latitude and longitude are angles measured in degrees from the Earth’s center to a point on the Earth’s surface.
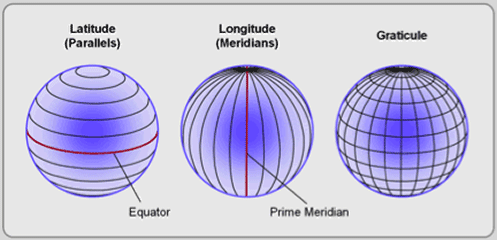
Figure 3.2: Latitude, longitude, and the Earth’s graticule.
Midway between the poles, the equator stretches around the Earth, and it defines the line of zero degrees latitude (left image in Figure 3.2). Relative to the equator, latitude is measured from 90 degrees at the North Pole to -90 degrees at the South Pole. The Prime Meridian is the line of zero degrees longitude (center image in Figure 3.2), and in most coordinate systems, it passes through Greenwich, England. Longitude runs from -180 degrees west of the Prime Meridian to 180 degrees east of the same meridian. Because the globe is 360 degrees in circumference, -180 and 180 degrees is the same location.
Earth’s Shape
If the geographic extent of your project area was small, like a neighborhood or a portion of a city, you could assume that the Earth is flat and use no projection. This is referred to as a planar surface or even a planar “projection,” but with the understanding that it does not use a projection. Planar representation does not significantly affect a map’s accuracy when scales are larger than 1:10,000. In other words, small areas do not need a projection because the statistical differences between locations on a flat plane and a 3-dimensional surface are not significant.
For small-scale maps (those that encompass a large area, see Figure 2.3), you must consider the Earth’s shape. Our assumption that the Earth is round or spherical does not accurately represent it. The Earth’s constant spinning causes it to bulge slightly along the equator, ruining its perfect spherical shape. The slightly oval nature of the Earth’s geometric surface makes the terms ellipsoid and spheroid more accurate in describing its shape, but they are not perfect terms either since differences in material weights (for instance iron is denser than sedimentary deposits) and the movement of tectonic plates makes the Earth dynamic and constantly changing. The Earth is a geoid with a slight pear shape; it is a little larger in the southern hemisphere and includes other bulges. The difference, however, between the ellipsoid and the geoid is minor enough that it does not affect most mapping. Until recently, projections based on geoids were rare because of the complexity and cost of collecting the necessary data to create the projection, but satellite imagery has helped with measurement and geoid projections are now more common.
Map Projections
Globes do not need projections, and even though they are the best way to depict the Earth’s shape and to understand latitude and longitude, they are not practical for most applications that require maps. We need flat maps. This requires a reshaping of the Earth’s 3-dimensions into a 2-dimensional surface. This reshaping cannot be done without introducing some error. To illustrate this point, imagine taking a cardboard globe, cutting it in half at the equator, and then cutting both the northern and southern hemispheres into four equal parts apiece. Resting on a table, the pieces are not flat; they arch in the center. Try flattening one of the pieces. If you succeed, part of the cardboard will be scrunched together and other parts will tear apart. By flattening it, you modify its geography.
Map projections enable the reshaping of the Earth by mathematically transforming spherical coordinates (x, y, and z) to 2-dimensional (x and y) space. They are the foundations we use to represent the Earth’s surface or portions of it.
Projections are abstractions, and they introduce distortions to either the Earth’s shape, area, distance, or direction (and sometimes to all of these properties). Different map projections cause different map distortions.
One way to classify map projections is to describe them by the characteristic they do not distort. Usually only one property is preserved in a projection. This chapter confines its focus to just two properties—area and shape—because the projections that preserve these properties—equal-area and conformal—are the most common.
Equal area (or equivalent) projections preserve the area (or the amount of space) within features. On a small-scale political map of the world, the areas within each country are preserved. In reality, the area of Mexico and Greenland is similar, and in the right-hand map in Figure 3.3, which is drawn in an equal area projection called Mollweide, the two territories are approximately the same size. Equal area projections, however, distort all the other properties. Shape, distance, and direction are not preserved.
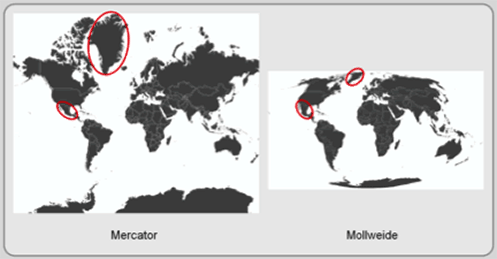
Figure 3.3: Projections transform the 3-D Earth into a 2-D plane. Some projections, like Mercator, attempt to preserve area while other projections like Mollweide preserve the area contained within the landmasses.
Conformal (also known as orthomorphic) maps preserve shape by preserving the angles of feature boundaries like countries and continents. Maintaining angles, however, distorts the area within the features (see left map in Figure 3.3). In the Mercator projection, Greenland looks like Greenland, but it is far larger than Mexico, its spatial equivalent. In addition, no conformal projection preserves the shapes of features that extend close to the poles (notice Antarctica).
Another way to classify map projections is by their projection surface. Imagine a translucent globe with country boundaries and latitude and longitude lines drawn upon it in black. In addition, imagine a light bulb positioned at the globe’s center. If you placed large pieces of paper on or around the translucent globe and turned on the interior light, you would see the country boundaries and the latitude and longitude lines projected onto the paper. If those projected lines were imprinted onto the paper, the paper could be removed from the globe, cut, and flattened to produce a 2-dimensional map.
What you just imagined is the way many projections were first conceived. Even today, in the age of computer modeling, most of the map projections we use are variations on three basic projection surfaces: planar, conic, and cylindrical (see Figure 3.4).
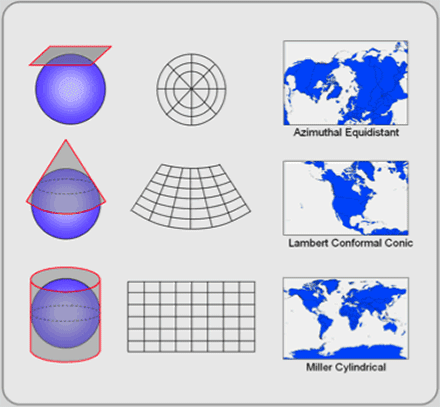
Figure 3.4: Projection surfaces.
Planar projections, the least common, can be conceptualized by placing a flat sheet in contact (at one point) with the translucent globe, usually at the North or South Pole, and the lines on the globe are projected onto the sheet. The projected map creates a circular graticule (see top row of Figure 3.4). Direction, one of the properties not described, is usually preserved from the center of the map outward. Some planar projections preserve area or distance. Consider using a planar projection if your research area is at one of the poles.
- Conic projections, a common projection surface, are conceptualized by placing a paper cone on the globe, and the lines on the globe are projected to the cone. After unraveling the cone, the graticule appears fan shaped (middle row of Figure 3.4). Conic projections preserve different properties including area and shape, but never both in a single projection. Distortion across the map varies. No distortion exists along the parallel (latitude) where the cone touches the globe, but distortion increases in both directions away from this line of tangency. Consider using a projection with this surface if your study area is in the mid-latitudes including the U.S.
- Cylindrical projections are developed by wrapping paper around the globe in the shape of a cylinder. The lines on the globe are projected to the cylinder (bottom row of Figure 3.4), and the resultant graticule is rectangular. There is no distortion along the equator (its point of tangency), but distortion increases toward the Earth’s poles. This projection surface preserves different properties including area and shape (but again, both are not preserved in a single projection). Consider using this projection surface if your study area is worldwide or in the tropics.
Many variations can be made using these three projection surfaces. Instead of having the paper come to a simple point or line of tangency with the globe, you could cut the globe’s surface (called secant), so that conic and cylindrical projections intersect the globe at two lines (latitude) and plane projections create a single circle. No distortion occurs anywhere the projection surface (the paper) intersects with the globe. Where the projection surface is outside the globe, features appear larger than they are in reality. Where the projection surface is inside the globe, features appear smaller.
Additional variations result when you move the position of the globe’s interior light or combine multiple projection surfaces. In addition, with computers, mathematical projections not based on these projection surfaces exist, and some of these projections are very popular.
There are thousands of different projections, but only a few dozen projections are noteworthy and used. Examples include Albers Equal Area Conic, Lambert Conformal Conic, Mercator, Miller Cylindrical, and Robinson. Many of these projection names include words like equal area, conformal, conic, and cylindrical; they provide clues to the projection’s characteristics and projection surfaces.
As mentioned in Chapter 2, it is important to choose an appropriate projection for your GIS project to achieve accurate results. Are you interested in calculating the area of features? If so, you must use a projection that preserves area, or your calculations will be inaccurate. Improper projections distort attribute accuracy, positional accuracy, and thus the information in your final maps and reports. As Chapter 6 describes, choosing an unsuitable map projection is one way to lie with maps.
How accurate do your locations need to be? If you are making a world map with the locations of the largest ports, precise locations are probably not necessary. If you are drilling a train tunnel, however, positional accuracy is required. Some projections use spheres to model the Earth’s shape. Remember (from the first part of this chapter) that a sphere is the most generalized shape of the world and the least accurate. Many projections are based on spheres, and these projections are suitable for world maps and large world regions that do not require a high degree of positional accuracy. Most projections today, however, are based on ellipsoids (and spheroids) that distort the uniformity of the sphere to bulge a bit at the equator. Statistically speaking, there is no significant difference between most ellipsoids and the true shape of the Earth for most mapping purposes. Still, for those projects that require even more precision, there are projections based on geoids. These projections were rare until recently because of the time it took to calculate the projections and the difficulty of the math and measurement. With increasing satellite imagery, however, they are more common.
Coordinate Systems
Projections and coordinate systems are two separate things. As described above, projections convert the Earth from 3-dimensional space to a 2-dimensional map. Coordinate systems are referencing systems used to describe specific locations and measure distances on maps. They provide x, y locations (sometimes designated as Eastings and Northings) for features, and, within GIS, they are used to spatially register layers of features that occupy the same area.
While coordinate systems are not projections, they usually use them. Latitude and longitude, the best known coordinate system, however, does not use a projection, but in most cases, coordinate systems incorporate a map projection, reference spheroid, datum, one or more standard parallels, a central meridian, and possible shifts in x or y (easting and northing) directions.
Like projections, there are many coordinate systems. Some of these coordinate systems focus locally and some globally. The most common at the world level is latitude and longitude, but because it is not a “projected” coordinate system, plotted points usually have a high degree of distance and shape distortion when plotted on a 2-dimensional flat map (and so it should not be used for making two-dimensional maps). Latitude and longitude uses the Prime Meridian and the Equator as reference planes, and it is best used when conceptualizing the Earth as a globe.
There are two ways of providing latitude and longitude coordinates. One method uses degrees, minutes and seconds. For instance, the CSUS Geography department is located at 38*N 33’ 32” latitude and 121*W 25’ 31” longitude. Another method is decimal degrees, and the same coordinates are represented as 38.55889 latitude and -121.42527 longitude.
The following is a description of a few of the most used coordinate systems in the United States: Universal Transverse Mercator, State Plane Coordinate System, and United States National Grid. Latitude and longitude, also widely used, was described earlier in this chapter.
Developed in the 1940s by the U.S. Army Corps of Engineers, Universal Transverse Mercator (UTM) is a coordinate system that largely covers the globe. The system reaches from 84 degrees north to 84 degrees south latitude, and it divides the Earth into 60 north-south oriented zones that are 6 degrees of longitude wide (see Figure 3.5). Each individual zone uses a defined transverse Mercator projection. The contiguous U.S. consists of 10 zones. In the Northern hemisphere, the equator is the zero baseline for Northings (Southern hemisphere uses a 10,000 km false Northing). Each zone has an arbitrary central meridian of 500 km west of each zone’s central meridian (called a false Easting) to insure positive Easting values and a central bisecting meridian. In UTM, the CSUS Geography Department is located at 4,269,000 meters north; 637,200 meters east; zone 10, northern hemisphere.
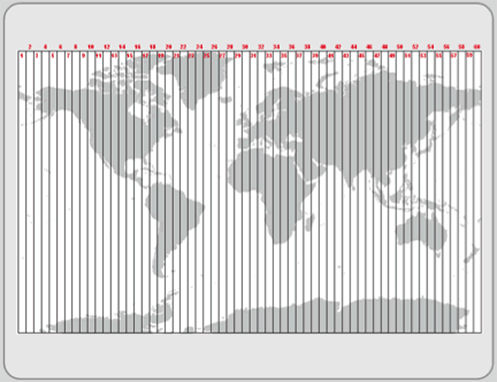
Figure 3.5: Universal Transverse Mercator zones.
The State Plane Coordinate System (SPCS) is a projected coordinate system that divides the U.S. and its possessions into over 120 zones (see Figure 3.6). Some smaller states use a single zone while larger states are divided into several zones. California has six zones (see map in lower-left corner of Figure 3.6). Each zone provides a local reference system that has its own parameters. Zones oriented east to west use the Lambert Conformal Conic projection while zones stretching more north to south use Transverse Mercator (not to be confused with UTM). Used principally by cities, many counties, and some states, they are popular projected coordinate systems. In SPCS, the CSUS Geography Department is located at 599200.796 feet; 2050091.975 feet; CA zone 2.
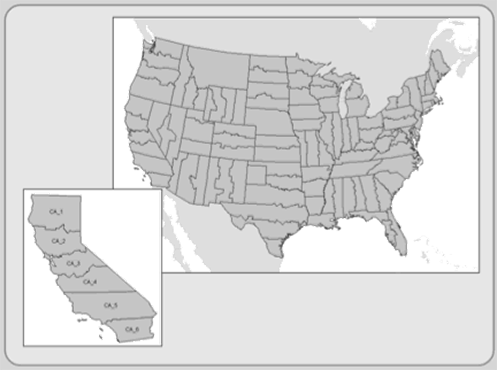
Figure 3.6: State Plane Coordinate System.
Many GIS projects cover more than one SPCS or UTM zone. In response to calls for a single coordinate system that covers the entire U.S., the United States National Grid (USNG), was created in 2001. After the attacks of September 11, 2001 and the increasing use of GPS-enabled and location tracking devices, a consistent grid takes on additional importance, and in 2005, the Department of Homeland Security (DHS) recommended that any DHS grant should reference their data to USNG. USNG incorporates the U.S. Military Grid Reference System’s hierarchy (not described here), but the basic zones are identical to UTM.
Datums
A datum is a starting point for locating features on the Earth’s surface; it is the origin point of a coordinate system. It defines the position of the ellipsoid (or spheroid) relative to the Earth’s center. There are many different datums and hence many different starting positions. Like both projections and coordinate systems, international organizations and individual nations have established datums for their specific needs. The World Geodetic System 1984 (WGS84) is the most widely used datum internationally. In the U.S., the two most used datums are North American Datum 1927 (NAD27) and North American Datum 1983 (NAD83). NAD83 updates NAD27 by using a more accurate ellipsoid for North America, derived from better satellite imagery, and changing reference units from feet to meters.
MAP PREPROCESSING
Map preprocessing functions are housecleaning tasks that make the data you input into the GIS usable for data analysis. The objective is to get all of your GIS datasets into the same projection, and then to make each layer spatially in tune with each other. Many map-preprocessing tasks do just and include reprojection, georeferencing, resampling, reclassification, and edge matching. In addition, verifying, editing, and manipulating your map features are part of this chapter as well.
Reprojection: Changing Projections, Coordinate Systems, and Datums
All of your project’s feature layers must be in the same projection and coordinate system if you intend to use them for analysis or map production. Both raster and vector GIS programs allow you to convert layers of features from one projection, coordinate system, and datum to another. In vector systems, it involves translating the x and y coordinates of all the features to new coordinates. In raster systems, it involves coordinate translation and resampling the pixels of one image into a new image (in some raster-based systems, changing projections is called resampling). For both vector and raster systems, the processes are not error free and datasets that are repeatedly translated back and forth compound errors.
All GIS programs have projection utilities that allow you to change your layer’s projection, coordinate system, and datum. When reprojecting data, you need to know both the existing and the output projection parameters (parameters include projection, coordinate system, and datum). Existing projection information is found in the layer’s metadata if it exists. If metadata does not exist, you need to speak with someone who created or at least uses the data set. As for the output projection parameters, presumably, you know these (this should be determined in the planning phase). When reprojecting, many programs give you the option to import your projection parameters by selecting an existing GIS layer that already uses them. If you choose this option, the GIS program takes the selected layer’s parameters and establishes them in the reprojected layer. This saves time especially if you have multiple layers to reproject.
Georeferencing
Any scanned image can be entered into a GIS, but to be useful, the image needs to be placed in its proper geographic location. Georeferencing aligns images to their spatial location. This process is common due to the popularity of “heads up” digitizing (described in Chapter 2).
Georeferencing is typically done by aligning the image to existing projected feature layers that are in their correct position. Since any scanned image is fundamentally a matrix of pixels, georeferencing the raster layer involves moving and stretching this matrix so that it rests at its true location (see Figure 3.7). To do this, you need to load the unprojected image and the projected feature layers and—in order—select corresponding control points, which are locations you can distinguish on both the image and the feature layers (left map in Figure 3.7). For greater accuracy, select as many control points as possible and make sure they are scattered throughout the image. If they are clustered in a corner of the unprojected image, only that part of the image will be georeferenced properly.
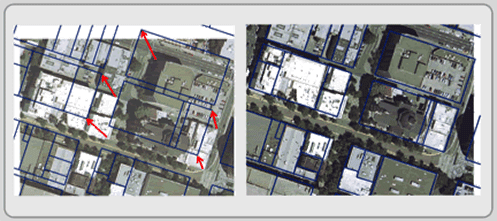
Figure 3.7: Georeferencing an image to its real-world location. The left map displays both the image we want to move and the area's parcels. The red arrows represent the corresponding points where you want to move points in the image. When the georeferencing is complete, the image will be at its real-world location.
Georeferencing assigns coordinate information about where the image rests in relation to the Earth’s surface. When you save your georeferenced image, a “world” file is created. This is an ASCII text file that has the exact name of your image file but with a different yet related file type. For example, if you have a TIFF image called Mexelev.tif, the world file (called a GeoTiff file) will be Mexelev.tfw. The “w” at the end of the file type denotes its status as a world file. Most GIS software packages are able to interpret these files and display the images in their proper location as long as the file names are the same and the two files are located in the same directory.
The first column of Figure 3.8 is an example of a world file. It has six lines with locational values. The second column describes what the six locational values are, and it is not contained in the world file.

Figure 3.8: Typical world file format.
Resampling
As briefly mentioned above, resampling changes raster layers from one projection to another, but it can also be used to transform the resolution of raster images. For example, resampling can convert each 2 by 2 array of pixels (4 pixels total) into a single but geographically larger pixel. To accomplish this, it changes the pixel’s attribute values with mathematical formulas to best approximate the attribute values for the new layer. For instance, it might average the four numeric values and place the mean in the single resampled pixel that replaces them in the new image. In Figure 3.9 below, the image to the right is a generalized resampling of the image to the left. Resampling is important if you are working with multiple raster images with varying resolutions. You need to translate your images to a common resolution (much like a common projection) to analyze them.
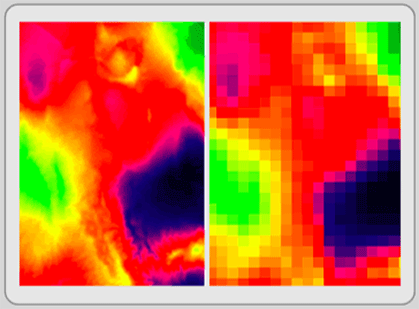
Figure 3.9: Resampling. The original image on the left had a pixel resolution of 250 meters. The resampled image on the right has a resolution of 2500 meters.
Reclassification
Reclassification generalizes values in a raster layer to highlight broader classes. This popular preprocessing technique re-assigns values in an input raster layer to create a new, more generalized, raster layer. Reclassification changes pixel values based on a criterion that you specify. In Figure 3.10, a raster image that denotes land covers is reclassed into two values. Reclassifying the database may reveal broader patterns by removing the layer’s unique classes. Reclassification is also commonly used to convert interval and ratio attribute pixel data into ordinal data used in the overlay process.
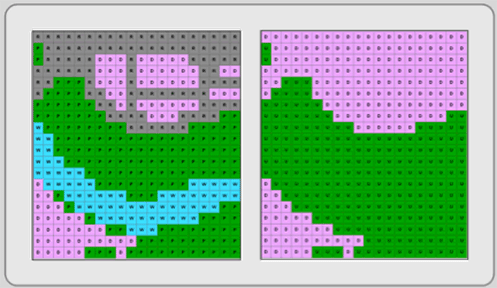
Figure 3.10: Reclassification. The image on the left depicts 4 different land covers. The image on the right aggregates land covers (D and R become D; P and W become U) into two classes. Image by Mike Tuck.
Edge Matching
When side-by-side map layers are retrieved and displayed, they might not line up well with each other (see Figure 3.11 below). Edge matching adjusts the location of features that extend across one map’s boundaries into another.
Edge matching requires your input in matching together the common edge of the two maps. The features that you believe are positioned correctly are usually “anchored” down, and the remainder of the map is moved, stretched or contracted like a sheet of rubber to line up the features on the maps. The map features, except those that are anchored, are spatially adjusted.
Which map features should you anchor down and which should be stretched? It is not an easy question. The answer might be found in the layer’s metadata. Perhaps one layer was entered at a coarser (less accurate) scale or with less precision. If, however, the properties and author of the two layers are identical, you should use a third layer (perhaps a georeferenced aerial photograph) that you have some confidence in to check the positional accuracy of the features within these two layers. When all else fails, you might have the features split the difference.
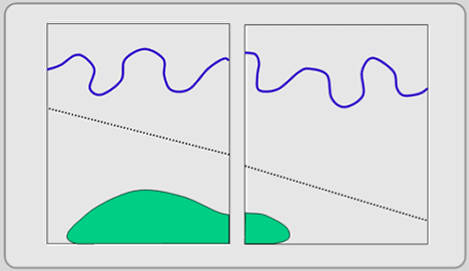
Figure 3.11: Edge matching. Sometimes two maps that should fit up against each other do not. Edge matching manipulates one of both of them until they do.
Conflation
Conflation is similar to edge matching with one difference: It does not rectify the placement of features across maps. Instead, it tries to rectify feature locations within a single raster image. For that reason it is also referred to as rubber sheeting. It is an interactive process where you tack down features that are positioned correctly and move the remainder to more accurate locations.
Tiling
Sometimes workspaces get large; geographically they can be vast and thematically numerous. Tiling involves breaking up your workspace into more manageable and logical geographic subunits. Tiling subdivides existing layers (both the geography and the attributes) by geographic units. Figure 3.12, displays a portion of the U.S.G.S. topographic map grid across California. Tiling can be done by splitting existing layers with the larger geographic boundary or it can be planned from the outset of the GIS project. The GIS then maintains a library of all the tiles that represent the project area.
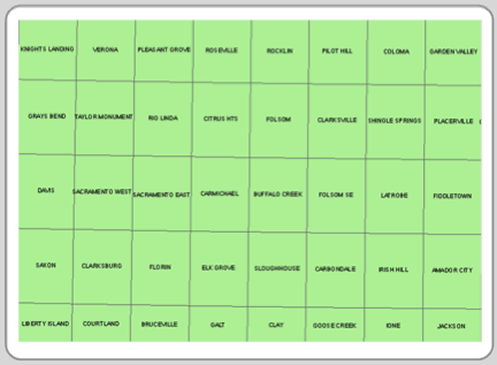
Figure 3.12: U.S.G.S. quadrangle maps for a portion of California.
Vectorization and Rasterization
These two common processes switch feature layers between vector and raster. For example, you might digitize data into a vector format but want to use it in a raster form. Vector layers are converted to raster by a process known as rasterization (see A in Figure 3.13). Alternatively, raster data can be converted to a vector layer through vectorization (see B in Figure 3.13).
Like any translation, it is not error free. Think, for example, of converting points from vector to raster. Each precise point location in the vector layer swims in the pixel of the new raster layer in which it now belongs. The precise spatial locations of the points are lost because the points now reside in much larger areas, which are determined by the pixel’s resolution. Now convert the new raster point layer back to vector. The points in the resultant vector layer are located at the center of each pixel in which they were contained. Comparing the new and original vector layers, you would see that they resemble each other but do not line up exactly.
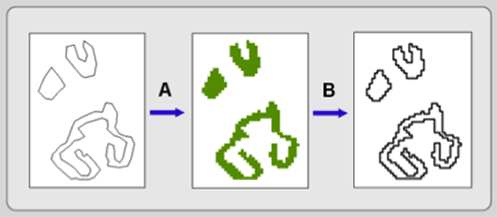
Figure 3.13: From vector to raster to vector again. Converting a vector file to raster is called rasterization (process A). Converting from raster to vector is vectorization (process B). Notice the differences between the first and third maps, both vector layers.
Coordinate Thinning
Coordinate thinning (also known as map generalization) generalizes or “smoothes” feature shapes by removing nodes (vertices) from line and polygon features. It reduces layer storage size, and it can be used to remove unwanted detail from map features. Sometimes detail held in a layer is not always appropriate for a small-scale map. For example, in the top map of Figure 3.14, notice how the detail of portions of the coastline resembles ink blobs because of the amount of coastal detail. The detail may take away from the map’s purpose. If one were to enlarge the image, the detail might be welcomed. By thinning the vertices along the coast, the map becomes simpler and clearer (bottom map in Figure 3.14). Perhaps this map is too generalized at this scale. Notice that a couple of islands have disappeared.
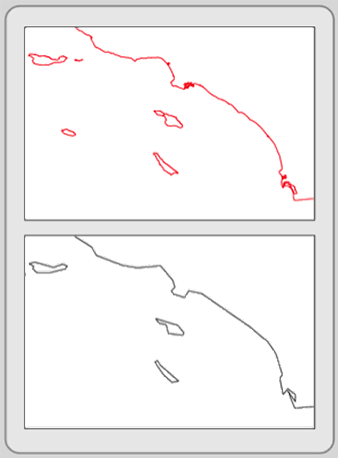
Figure 3.14: Coordinate thinning. Notice the differences in detail.
Topological Functions
Topology, the spatial relationships among features, focuses on where features are in relation to one another and how they are related to one another. Focusing on how features relate to each other, topological functions (a semi-automated process) help you clean up your layer’s spatial errors and determine what parts of different features are shared, contained, or connected to other features. In other words, these functions build topology. Most vector-based systems provide routines that help you find the following common topological problems (see Figure 3.15):
- Slivers, the most common topological problem, are small polygons that occur when either shared boundaries are entered separately for contiguous polygons or when the features of two layers are overlaid but do not match precisely. Topological functions can remove many of these slivers and reconcile common boundaries.
- Overshoots and undershoots usually occur when features are entered without the aid of a snapping routine. The feature vertices extend beyond (overshoots) or just short of (undershoots) their intended location. Topological functions can clean up these errors when you define a distance tolerance. If within the distance, the overshoot or undershoot snaps the vertex of one feature to the vertex of another feature.
- Redundancy occurs when two or more features in the same layer share the same node (vertex) or line but the layer duplicates these nodes (vertices) and lines. Layers should only store one node or line, which prevents duplication that could lead to errors. Most GIS programs have automatic elimination routines to eliminate duplicates.
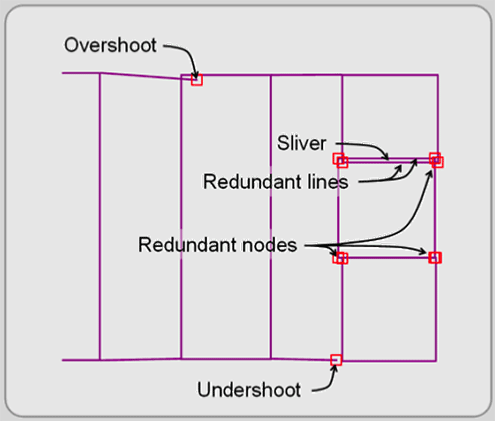
Figure 3.15: Typical topological errors.
MAP VERIFICATION & EDITING
Within each of your GIS layers, you need to identify and edit errors. This applies not only to your primary and secondary datasets, but also to every layer you preprocess and create as the result of analytical functions (those discussed in Chapter 5). Many spatial errors are the result of careless digitizing, inaccurate source maps, or a change in the area’s geography (like new buildings, boundaries, and forest fires).
Map Verification
This section looks at identifying and editing spatial errors. The last section of the next chapter deals with database errors. Map verification includes the following three steps:
- Visual examination. Use your eyes and your familiarity with the study area and the subject matter to check the spatial locations of features. In this step, verify that all of the features are present, in their correct location, and that they are the correct size and shape. Make sure that no extra features are present that do not exist (see Figure 3.16). Examine vector layers by loading a georeferenced and accurate reference image (an aerial photography or a Digital Orthophoto Quadrangle (DOQ)) under the layer you are verifying. For raster images, compare the layer with other accurate raster layers and visually overlay vector layers. If you are familiar with the subject matter and the study area, you can pick up many errors during this step.

Figure 3.16: Map verification: 1 = layer is missing building. 2 = building's position needs to be altered. 3 = layer may be missing buildings (check with additional sources or field check). 4 = layer depicts building that does not exist.
- Cleaning lines and vertices. This process is usually done by software first and interactive editing second. The software’s cleaning applications may include coordinate thinning and topological functions (see above).
- Comparison with source document. Although visual examinations pickup many errors, compare the layer’s completeness, position, size, and shape directly with the original hard-copy document. To do this, you can plot the layer you are verifying at the same scale as the original document, and with the help of a light table, superimpose the layer that you are verifying over the original and note the discrepancies. Take your time with this step; systematically check off each feature. Again, like in step 1, using an additional, high-quality layer to independently verify the position of features is a good idea especially if you have any doubts about the quality of your original map.
Data Editing
Spatial data editing involves adding, deleting, moving, and changing the shape of features. Data editing fixes the errors you find during the verification process. Each GIS program has its own particular way of editing the location of features (or a portion of a feature). Besides the elimination of slivers, overshoots, undershoots, and redundant nodes and lines, you may need to merge features, split features, and simply move individual nodes (vertices).
To make clean edits, know how to use your program’s snapping routine. When entering or editing contiguous or connected features, snapping moves your cursor slightly to align it with an existing node (vertex). This reduces overshoots, undershoots, and redundant points and lines.
While all GIS packages have entering and editing capabilities, many programs do not make editing (and entry) easy or intuitive. Because of this, many GIS users import their feature layers into CAD systems for detailed editing and data entry. CAD programs have specialized, easy-to-use tools for editing features. Why is CAD easier for entry and editing? They were created for precise drawing and drafting. GIS programs usually focus on compiling layers and on analyzing them. Many agencies and companies that use both CAD and GIS programs often refer to their CAD programs as legacy systems—an adjective that refers to their past prominence and infers that their organization is moving away from them. Many organizations, however, recognize CAD’s superior data entry capability and expect to keep these systems at least for a while.
Geometric Conversion
Geometric conversion consists of routines that change feature types between points, lines, and polygons. Perhaps the most frequent geometric transformation is the conversion of lines to polygons. This happens a lot because many CAD programs often use line segments to build parcels (and other features), but within a GIS these features are best coded as polygons. Another routine changes points to contours (lines), which are used to portray surface relief as a set of lines that connect points of the same value. Conceptually, contours are “threaded” through the points (or pixels) along approximate lines of constant value. Points are also frequently produced from polygons. This routine creates a “centroid”, a central point, usually placed at the intersection of the north-south and east-west mid points.
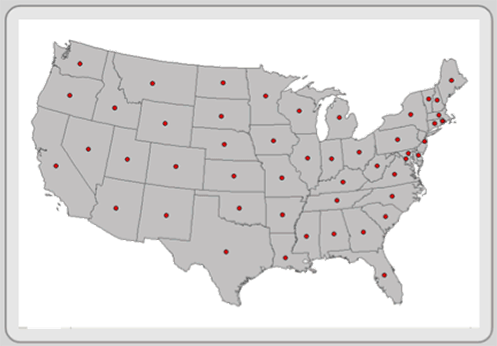
Figure 3.17: Creating centroids (point features) from polygons. The process automatically places a point at the half way mark of both its west-east and north-south range. In some cases, this places the state's centroid outside of its polygon. Many of the centroids in the above map have been moved to more of a visual center.
