Ch. 5: Analysis
INTRODUCTION
Once the data input process is complete and your GIS layers are preprocessed, you can begin the analysis stage. Analyzing geographic data requires critical thinking and reasoning. You look for patterns, associations, connections, interactions, and evidence of change through time and over space. GIS helps you analyze the data sets and test for spatial relationships, but it does not replace the necessity for you to think spatially. First, you must conceive of the possible spatial patterns and relationships. This chapter provides an overview of the most common analysis functions and continues the spatial analysis discussion started in Chapter 1.
By integrating GIS layers, you can ask the spatial questions outlined in Chapter 1: “What is at…?”, “Where is it…?”, “What has changed since?”, “What spatial patterns exist?”, and “What if…?” (the scenario question). The first two of these questions inventory features and minimally examine feature location and relationships. The last three questions are more complex. To answer these questions, you must use or string together some of the analytical functions that you will learn about in this chapter. The particular analytical functions—and their order—are up to you.
This chapter focuses on the GIS functions that assist you in analysis—that help you evaluate, estimate, predict, interpret, and understand spatial data. The chapter breaks down these functions into four analyses presented in Figure 5.1:
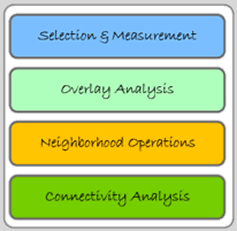
Figure 5.1: Analysis functions categories.
Many of the specific analyses contained in the above categories have multiple names for the same function. This chapter uses the most frequently used terms, but attempts to note commonly used synonyms. It also notes whether the analytical processes are vector-based, raster-based, or can be used with both data models.
SELECTION & MEASUREMENT
The selection part of this category barely justifies its placement in this chapter. Selection is not an analysis function, but it is an important first step for many analysis functions. Due to its heavy use in the analytical phase, however, it is included. The following two selection processes, attribute query and spatial selection, have been discussed to some degree earlier in this text. Measurement, the second part of this category, is easier to justify as an analytical process because numbers that describe features are generated by these functions.
Attribute Query (Boolean Selection)
As described in Chapter 4, attribute query selects features based on their attribute values. It involves picking features based on query expressions, which use Boolean algebra (and, or, not), set algebra (>, <, =, >=, <=), arithmetic operators (=, -, *, /), and user-defined values. Simply put, the GIS compares the values in an attribute field with a query expression that you define. For example in Figure 5.2, if you want to select every restaurant whose price is considered inexpensive, you would use a query expression like “PRICE = $” (where “PRICE” is the attribute field under investigation, “=” is the set algebra operator, and “$” is the value). Your software then looks for a value equal to $ in the price field of each record, and selects only those records that satisfy the equation. In Figure 5.2, fifty out of 112 restaurants fit the query expression and are selected within the attribute file. They are simultaneously highlighted on the map.
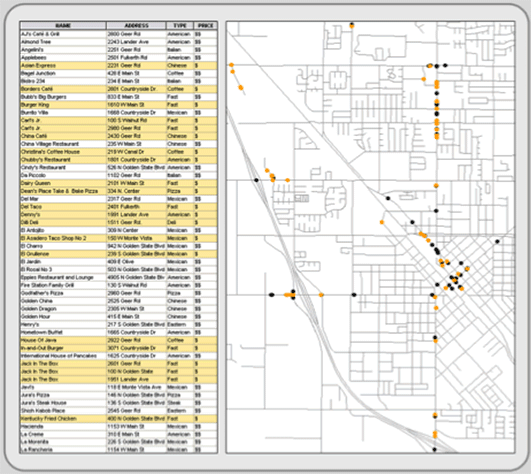
Figure 5.2: Selecting by attribute. In this example, restaurants are selected on their price being inexpensive (PRICE = ‘$’). The results are displayed both on the map and in the attribute table (highlighted in orange).
Attribute queries can be complex. Query expressions, like the one above, can be strung together to form long equations that could include any of the operators listed above and any number of existing attribute fields. Once the desired features are selected, you can perform a number of analytical processes on just the selected features, or, alternatively, you could save the highlighted features to a new layer.
Attribute query is a vector process, but reclassification (discussed as a preprocessing function in Chapter 3) is a similar raster-based process.
Spatial Selection (Spatial Searches)
While attribute queries select features by sorting through records in a data file, spatial selection chooses features from the map interface. In most cases, it selects features from one layer that fall within or touch an edge of polygon features in a second layer (or an interactively drawn graphic polygon). Figure 5.3 is an example that uses the same restaurant layer as the previous figure. Again, the first layer consists of restaurants, some of which one wants to select. The second layer is composed of polygons radiating out from points of interest. After the selection process, the customers falling within the overlaying polygons are highlighted (selected). Ninety out of 112 restaurants fit the query expression and are selected within the attribute file and simultaneously on the map.
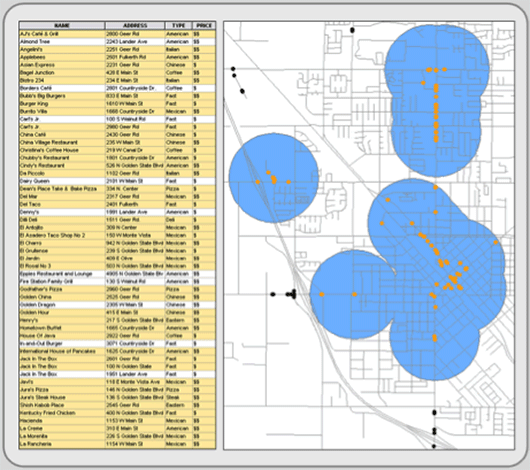
Figure 5.3: Spatial selection. Only those restaurants that fall within the blue polygons are selected.
There are many types of spatial selection. Point in polygon, perhaps the most used, selects the points of one layer if they are contained within a selected polygon (or polygons) of a different layer (or graphic). Line in Polygon, a similar operation, selects line features that are wholly or partially contained within a different layer’s polygon. Polygon in Polygon is another variation that selects polygon features within (or overlapping) selected polygons from a second layer. Another type of spatial selection is point distance (which has line and polygon versions too), which identifies all the points in one layer that are within a specified distance of a selected point(s) in a different layer. Like any type of selection, you can perform analytical processes on those highlighted features or save them to a new layer.
You can mix spatial selections and attribute queries. Here you might spatially select features first, and then from the feature’s attribute file, you would reduce (or alternatively increase) the selected records through attribute query expressions. Figure 5.4 is an example using the same restaurant data as above. Thirty seven out of 112 restaurants fit the query expression and fall within the overlaying polygons. They are highlighted both within the attribute file and on the map.
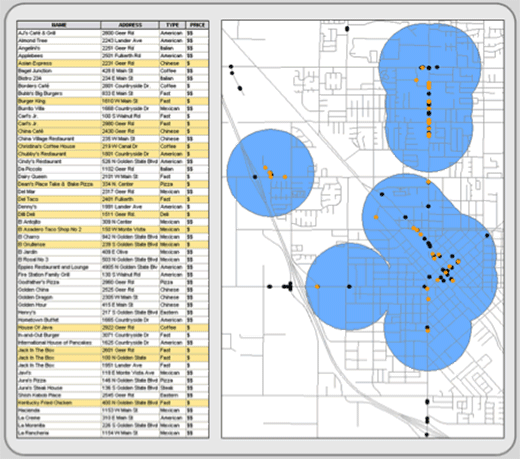
Figure 5.4: Spatial and attribute selection combined. In this example, restaurants that fall within the blue polygons and are inexpensive (PRICE = $) are highlighted in orange.
Spatial selection is a vector process, but when you combine reclassification (discussed in Chapter 3) and overlay (discussed later in this chapter), the combination produces a raster version of spatial selection.
Measuring Distance
There are many ways to measure distance. Most GIS programs, both raster and vector, have a ruler button that allows you to measure distances across a map. After clicking the button, you point on the map where you want to begin your distance measurement and then click at the ending point (or intervening points that define the path you want to measure).
Many vector-based systems measure distances along existing vector line networks, like streets, sewers, and railroads. This type of distance measurement relies on topological network relationships, which are discussed later (see Connectivity Analysis). In addition, some vector systems automatically generate length measurements for line features as you enter them. They store the length result in an attribute field within the layer’s data file. Those systems that do not have this automatic function usually provide a way for you to calculate line feature length and store the result in an attribute field that you define. Once calculated and stored, you can sum the length of multiple line features by selecting them and calculating their sum (see Calculating Descriptive Statistics below).
Raster-based systems allow you to generate distance measurements in all directions away from a selected pixel or group of pixels. These distances are placed in a new layer where each cell’s value represents the distance from that cell to the nearest selected pixel. These “distance” layers are often used for spread functions (see Spread Functions below).
Measuring Area/Perimeter
Many vector systems automatically generate area and perimeter measurements for polygon features and store these values in prescribed attribute fields. Those systems that do not have this automatic function do provide a way for you to generate area and perimeter and store the results in user-defined fields. See Figure 5.5 for an example. Once calculated and stored, you can select multiple polygon features and sum their area and perimeter (see Calculating Descriptive Statistics below).

Figure 5.5: Area and perimeter contained as attributes in the layer’s data file.
Calculating areas and perimeters are done differently in raster systems. Instead of measuring and storing each polygon’s area and perimeter in the feature’s pixels, raster systems already know the size—the area covered—by a single pixel. To calculate area, it simply adds up the number of pixels with a specified attribute and multiples the count by the area contained in a single pixel. It is easy math. For example, your layer might have 100 polygons that possess one of twelve land cover categories. The routine finds each occurrence of the twelve categories (even if they are not contiguous) and sums the category’s area and perimeter. Perimeter is usually equally easy if the pixels are square, and in the vast majority of cases they are. These measurements are provided either in standard tables or in new layers where the pixels exhibit the sums of the area and perimeter of the category to which it originally belonged.
Calculating Descriptive Statistics
Descriptive statistics summarize attribute data. They reduce the complexities of numerous individual values into a few meaningful numbers that describe the individual features collectively. Descriptive statistics are organized into two groups: measures of central tendency and measures of dispersion.
Central tendency describes the center of the attribute data’s distribution. The mean, median, and mode are its three common measures, but which measure you should use depends largely on the attribute’s level of measurement (described in Chapter 2). Figure 5.6 depicts the three central tendency measures for the attribute values of a single field.
- The most used measure is the mean (commonly referred to as average), which is calculated by adding together each feature’s attribute value and dividing the sum by the number of features. For example, if you wanted to characterize the age of the people reading this e-text, you would sum the age of each reader and divide it by the number of readers. The result is the mean. It—like all measures of central tendency—is a surrogate used to describe all the values within a single attribute field. This measure requires interval or ratio data.
- If we placed the attribute values in ascending or descending order, the median is the middle score in the distribution (this works for an odd number of cases). In other words, half of the attribute values are above and half are below this value. In an even numbered distribution, the median is the average of the two middle scores. Median is used for ordinal and derived (aggregated) data.
- Mode is the most frequent score in a distribution. Of course, some distributions do not have a mode if there are no repeated values. At times, the only repeated value might be at the low or high end of the distribution, making this measure a bit unreliable and certainly un-central. The measure, however, is helpful in describing leading categories (for instance the different political parties). It is the only measure for describing the central tendency of nominal data.
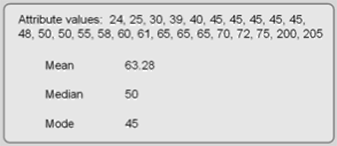
Figure 5.6: Central tendency measures. These attribute values attained from a vector layer’s attribute field or from selected pixels in a raster layer.
Dispersion, the second group of descriptive statistics, looks at the attribute data’s spread. Its measures (including range, variance, and standard deviation) describe how much the attribute values vary around the distribution’s center (its central tendency measures). Are the values clustered tightly or are they spread out? These measures help you judge how well the central tendency characterizes all of the values in the attribute field. If the measure of dispersion is small, the values are clustered and the central tendency measure describes the distribution well. There are several types of measures of dispersion (also see Figure 5.7):
- Counts and frequencies are not measures of dispersion, but they are basic ways to summarize data. Counting simply denotes quantity. Frequency is the number of times an attribute field has a particular value. A frequency distribution, usually in the form of a histogram, describes the shape (or structure) of the attribute data by tabulating the frequencies of each value (or range of values).
- Range is the distance between the minimum and maximum attribute values. To derive it, simply subtract the minimum value from the maximum value. It is the simplest measure of dispersion, but it is vulnerable to outliers (rogue values that are significantly different from the rest of the attribute values). If you think outliers affect the range, use the interquartile range instead. It divides the distribution, arranged from low to high, into four parts each containing 25 percent of the attribute values, and it is the difference between the 25th & 75th percentiles.
- The variance looks at the difference between the distribution’s values and its central tendency measure (in this case the mean). It is more complex than computing the average difference that each attribute value falls from the mean. Such a score does not provide enough numeric emphasis to the attribute values on the low and high end of the distribution. The variance adjusts for this by squaring the difference, summing the squares, and dividing by the count.
- Standard deviation is the square root of the variance. Like the variance, it describes the dispersion around the mean and allows you to evaluate how closely the numbers in the dataset are packed around the mean (in other words, how well the mean describes or summarizes the set of numbers). Similarly, the smaller the number the tighter the values are clustered around the central tendency measure. Unlike the variance’s higher values, however, standard deviation uses numbers that are similar to the original dataset. Still, the two are essentially the same thing.

Figure 5.7: Measures of Dispersion.
In vector systems, descriptive statistics are usually generated within the attribute file interface. In raster layers, menu commands process the descriptive statistics. Each attribute field can be summarized in its entirety or confined to selected records or pixels. Which descriptive statistics are calculated depends on the attribute data’s level of measurement (Figure 5.8).
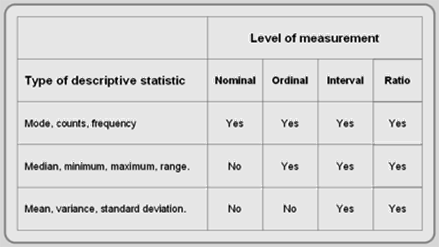
Figure 5.8: Depicts which descriptive statistics can be used with different data levels.
OVERLAY ANALYSIS
Overlay is one of the most common and powerful GIS functions. It investigates the spatial association of features by “vertically stacking” feature layers to investigate geographic patterns and determine locations that meet specific criteria.
It is the best-known GIS function, but examples of overlay predate computers and GIS. A simple but powerful example was described in Chapter 1: Dr. Snow overlaid water pumps over cholera deaths to see a spatial pattern and infer a connection between water and the disease. Other, more sophisticated, overlay analyses also occurred before the advent of GIS. In the 1960s, Ian McHarg sought a better way to plan land use, taking into account the physical environment and human factors. In Design with Nature (1969), McHarg formalized his site planning process based on overlay transparencies. He created hard-copy transparent maps for each relevant human (historic values, scenic vistas, social costs, etc.) and physical (slope, surface drainage, riparian areas, susceptibility to erosion, etc) factor. Each transparency included shades ranging from dark tones (areas with high values) to light tones (areas with low values). Physically, the transparencies were superimposed upon each other over the study area’s base map. A composite map revealed dark tones over areas where multiple layers had high values (high impacts) and light tones in regions with low impact values. McHarg felt that planners needed to undertake this process to determine which areas should be left natural and which places were suitable for development. His book and method were so popular that many of the first GIS projects attempted to formalize his technique using GIS.
Today, there are many types of GIS overlay. Vector and raster models both perform overlay, but their overlay functions differ considerably and thus will be discussed separately.
Vector (Logical) Overlay
Vector overlay predominantly overlays polygons in one layer over polygons in another layer, but it can also be used to overlay point or line features over polygon layers. Sometimes referred to as topological or logical overlay, it is conceptually and mathematically more demanding than raster overlay. There are three types of vector overlay operations:
Polygon on polygon is where one polygon layer is superimposed over another polygon layer to create a new output polygon layer. The resultant polygons may contain some or all of the attributes from the polygons in which they were created. Several types of polygon on polygon overlay exist, including intersection (A and B), union (A or B), and clip (A not B). These Boolean operators work both on the attribute table and the geography.
- Intersection computes the geometric intersection of all of the polygons in the input layers (see Figure 5.9). Only those features that share a common geography are preserved in the output layer. Any polygon or portion of a polygon that falls outside of the common area is discarded from the output layer. The new polygon layer can possess the attribute data of the features in the input layers.

Figure 5.9: Intersection of two layers.
- Union combines the features of input polygon layers (see Figure 5.10). All polygons from the input layers are included in the output polygon layer. It can also possess the combined attribute data of the input polygon layers.

Figure 5.10: Union of two layers.
- Clip removes those features (or portions of features) from an input polygon layer that overlay with features from a clip polygon layer (Figure 5.11). The clip layer acts as a cookie cutter to remove features (and portions of features) that fall inside the clip layer.

Figure 5.11: Clipping one layer from another.
Point in polygon is where a layer of point features is superimposed over a layer of polygon features. The two layers produce a point layer that includes attributes from the surrounding input layer polygons (Figure 5.12). Alternatively, you can tally the number of point features falling within each polygon and store the sum as a new attribute in the polygon layer. Other point attributes can be aggregated (summed, averaged, etc.) and included as attributes in the polygon’s data file. The transferring of attributes based on their geographic poistion is called a spatial join.
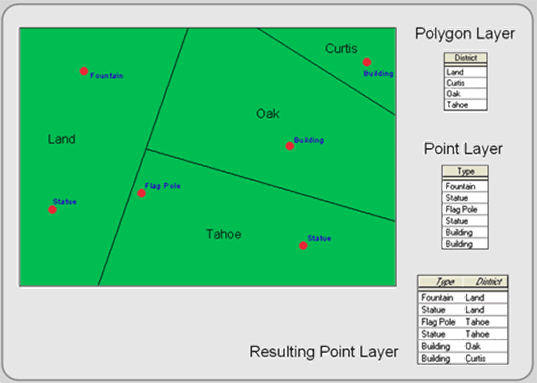
Figure 5.12: Point in Polygon.
Line on polygon is similar to point in polygon, but lines are superimposed on polygons. This type of spatial join either appends polygon attributes to line features falling within them or counts and aggregates line attribute data to the polygon layer’s data file.
Raster (Arithmetic) Overlay
Raster overlay superimposes at least two input raster layers to produce an output layer. Each cell in the output layer is calculated from the corresponding pixels in the input layers. To do this, the layers must line up perfectly; they must have the same pixel resolution and spatial extent. If they do not align, they can be adjusted to fit by the preprocessing functions discussed in Chapter 3. Once preprocessed, raster overlay is flexible, efficient, quick, and offers more overlay possibilities than vector overlay.
Raster overlay, frequently called map algebra, is based on calculations which include arithmetic expressions and set and Boolean algebraic operators to process the input layers to create an output layer. The most common operators are addition, subtraction, multiplication, and division, but other popular operators include maximum, minimum, average, AND, OR, and NOT. In short, raster overlay simply uses arithemetic operators to compute the corresponding cells of two or more input layers together, uses Boolean algebra like AND or OR to find the pixels that fit a particular query statement, or executes statistical tests like correlation and regression on the input layers (see Figure 5.13).
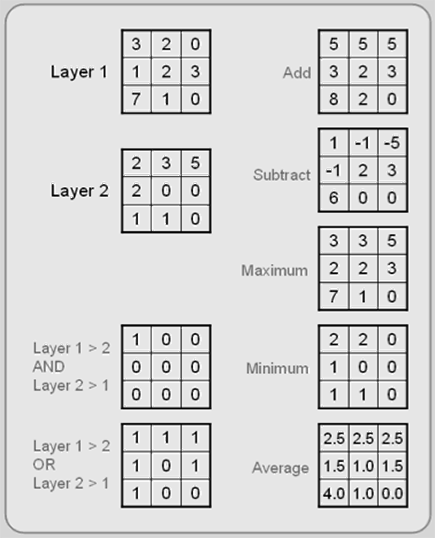
Figure 5.13: Raster Overlay. Using layers 1 and 2, all sorts of overlay are possible.
Correlation and Regression
Correlation and Regression are two ways to compute the degree of association between two (or sometimes more) layers. With correlation, you do not assume a causal relationship. In other words, one layer is not affecting the spatial pattern of the other layer. The patterns may be similar, but no cause and effect is implied.
Regression is different; you make the assumption that one layer (and its variable) influences the other. You specify an independent variable layer (sometimes more than one) that affects the dependent variable layer. Figure 5.14 shows a precipitation (dependent) and elevation (independent) as the layers.
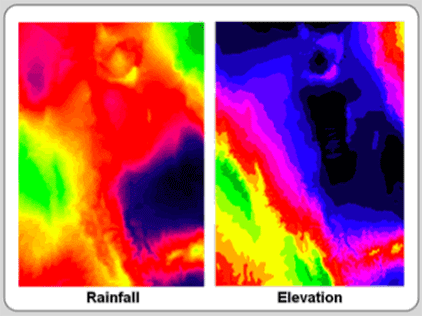
Figure 5.14: Is there a spatial relationship between these two layers? Correlation and regression tests allow you to overlay layers to test their spatial relationship.
With both statistical tests, you compute a correlation coefficient, which ranges from -1 to +1. Positive coefficients indicate that the two layer’s varaibles are associated in the same direction. As one variable increases, the other variable increases (both can simultaneously decrease too). The values closer to +1 describe a stronger association than those closer to zero. A negative coefficient depicts two layer’s variables that are associated but in opposite directions. As one variable increases, the other variable decreases. Values closer to -1 have a strong negative association. If the correlation coefficient is near zero, there is little to no association. Both of these processes are raster based.
NEIGHBORHOOD OPERATIONS
Neighborhood operations, also called proximity analyses, consider the characteristics of neighboring areas around a specific location. These functions either modify existing features or create new feature layers, which are influenced, to some degree, by the distance from existing features. All GIS programs provide some neighborhood analyses, which include buffering, interpolation, Theissen polygons, and various topographic functions.
Buffering
Buffering creates physical zones around features. These “buffers” are usually based on specific straight-line distances from selected features (like in Figure 5.15). Buffers, common to both raster and vector systems, are created around point, line, or polygon features. The resulting buffers are placed in an output polygon feature layer. Once complete, buffer layers are used to determine which features (in other layers) occur either within or outside the buffers (spatial queries), to perform overlay, or to measure the area of the buffer zone. They are the most used neighborhood operation.
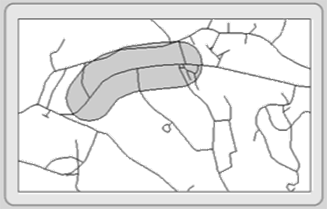
Figure 5.15: Buffering around a selected line feature.
Most buffers use constant widths to generate zones, but some buffers have variable widths that depend on feature attribute values. As an example, the figure to the right depicts a variable distance buffer based on decibels from an airport.
Interpolation
Interpolation is a method of predicting or estimating pixel values at unsampled locations based on the known values of neighboring pixels (see Figure 5.16). Since it is impractical for you to take measurements at all locations across your study area due to money, time, legal, and physical constraints, you interpolate between known pixel values (sampled locations). With interpolation, you create a continuous surface like elevation, temperature, and soil characteristics that occur everywhere. Because of its continuous nature, interpolation is only available within raster-based systems.

Figure 5.16: Interpolating between point features. The red dots are the points where values are known. The gray cells are the estimated data based on the known values.
There are many different types of interpolation: Linear interpolation, the simplest form, assumes that the value change over distance from recorded pixels is uniform. In other words, the value change per pixel is constant between two known points. This interpolation method is not always appropriate, so there are other methods including Fixed-radius Local Averaging, Inverse Distance Weighted, Trend Surface, Splines, and Kriging. All of these interpolation methods look at the values of the recorded pixels to generate the value of the pixels that fall in between. The methods differ in how they weigh the recorded attributes and in the number of observations used for each method. No method is accurate in every situation.
Theissen polygons (voronoi or proximal polygons)
Theissen polygons are boundaries created around points within a point layer (see Figure 5.17). The resultant polygons form around each of the points, and they delineate territories around which any location inside the polygon is closer to the internal point (that created it) than to any other point in the layer. Attributes associated with each point are assigned to the resultant polygon. It is a vector and raster process, but for more than one attribute, raster systems must use multiple layers.

Figure 5.17: Creating Theissen polygons from point features.
Topographic Functions
Topographic functions use Digital Elevation Models (DEMs) to illustrate the lay of the land. DEMs are raster layers containing elevation data in each pixel. From these values, you produce output layers to portray slope (inclination), aspect (direction), and hillshading (see Figure 5.18). These topographic functions are typical neighborhood processes; each pixel in the resultant layer is a product of its own elevation value as well as those of its surrounding neighbors.
- Slope layers exhibit the incline or steepness of the land. It is the change in elevation over a defined distance.
- Aspect is the compass direction in which a slope faces. From north, it is usually expressed clockwise from 0 to 360 degrees.
- Hillshading, which is cartographically called shaded relief, is a lighting effect which mimics the sun to highlight hills and valleys. Some areas appear to be illuminated while others lie in shadows.
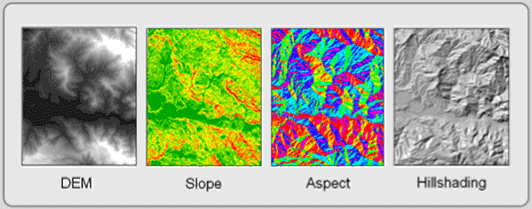
Figure 5.18: Topographic Functions. The DEM creates the slope, aspect, and hillshading layers.
While these functions are raster processes, most can be mimicked in a vector environment by Triangulated Irregular Networks (TIN). In addition, topographic functions can derive vector isolines (contours).
CONNECTIVITY ANALYSES
Connectivity analyses use functions that accumulate values over an area traveled. Most often, these include the analysis of surfaces and networks. Connectivity analyses include network analysis, spread functions, and visibility analysis. This group of analytical functions is the least developed in commercial GIS software, but this situation is changing as commercial demand for these functions is increasing.
Vector-based systems generally focus on network analysis capabilities. Raster-based systems provide visibility analysis and sophisticated spread function capabilities.
Spread Functions (Surface Analysis)
Spread functions are raster analysis techniques that determine paths through space by considering how phenomena (including features) spread over an area in all directions but with different resistances. You begin with an origin or starting layer (a point where the path begins) and a friction layer, which represents how difficult—how much resistance—it is for the phenomenon to pass through each cell. From these two layers, a new layer is formed that indicates how much resistance the phenomenon encounters as it spreads in all directions (see Figure 5.19).
Add a destination layer, and you can determine the “least cost” path between the origin and the destination. “Least cost” can be a monetary cost, but it can also represent the time it takes to go from one point to another, the environmental cost of using a route, or even the amount of effort (calories) that is spent.
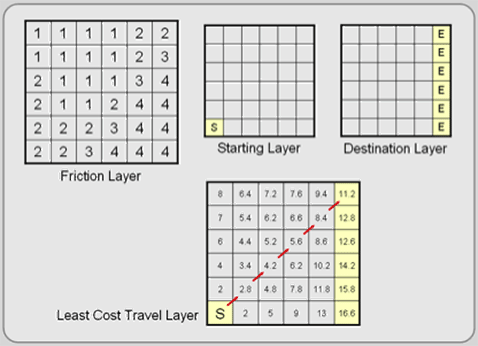
Figure 5.19: Spread Functions. This example shows that the shortest distance is not always the least cost distance.
Viewshed Modeling (Intervisibility Analysis)
Viewshed modeling uses elevation layers to indicate areas on the map that can and cannot be viewed from a specific vantage point. The non-obscured area is the viewshed. Viewsheds are developed from DEMs in raster-based systems and from TINs in vector systems. The ability to determine viewshed (and how they can be altered) is particularly useful to national and state park planners and landscape architects. Figure 5.20 depicts the areas within a park where a proposed radio antenna can be seen.
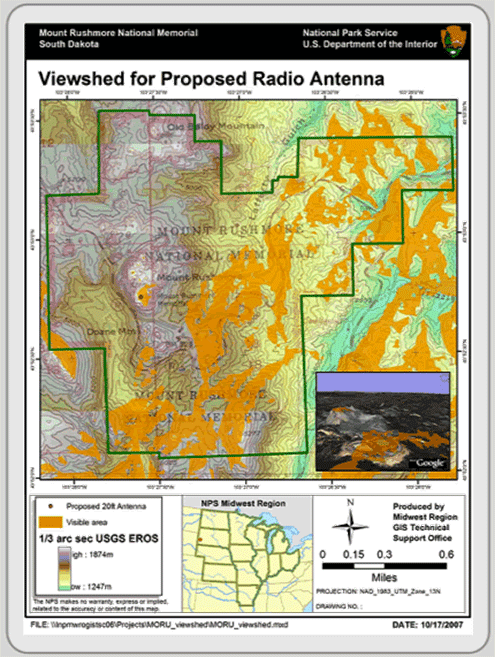
Figure 5.20: Viewshed Analysis. Map courtesy of the National Park Service, Department of Interior, 2007.
Network Analysis
Network analyses involve analyzing the flow of networks—a connected set of lines and point nodes (sometimes called centers or hubs). These linear networks most often represent features such as rivers, transportation corridors (roads, railroads, and even flight paths), and utilities (electric, telephone, television, sewer, water, gas). Point nodes usually represent pickup or destination sites, clients, transformers, valves, and intersections. People, water, consumer packages, kilowatts, and many other resources flow to and from nodes along linear features.
Each linear feature affects the resource flow. For example, a street segment might only provide flow in one direction (a one-way street) and at a certain speed. Nodes can also affect flow. A stuck valve might allow too much of a resource to stream out and away from its intended destination. Network analysis tools help you analyze the “cost” of moving through the network. Like spread functions, “cost” can represent money, time, distance, or effort. Network analyses are vector-based applications, but there are similarities with raster-based spread functions.
The three major types of network analyses include route selection (optimal path or shortest path), resource allocation, and network modeling.
- Route Selection attempts to identify the least “cost” route. As described above, cost can be defined a number of ways. You might want to find the shortest path between your home and a weekend destination or the least costly route that delivers UPS packages to their recipients. In any route selection routine, two or more nodes, including an origin and a destination point, must be identified and be able to be visited on the network. Sometimes there are a large number of possible routes. It is the job of the network analysis algorithm to determine the least cost route. Multiple paths are tested until the least cost path connects the starting and destination points.
- Resource Allocation, the second major type of network analysis, involves the apportionment of a network to nodes. To do this, you define one or more allocation nodes on the network. Territories of linear features, like streets, are defined around each of these allocation nodes. The linear features are usually assigned to the nearest node, where distance is measured in time, length, money, or effort. Figure 5.21 depicts 4-minute response times from six fire stations and three potential fire station locations. The polygon that is drawn around each station (triangle) represents the area that can be covered in 4 minutes.
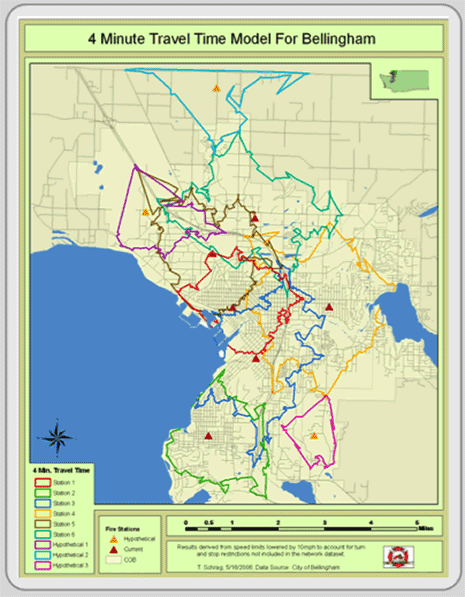
Figure 5.21: Resource allocation. Map is courtesy of Tyler Schrag, Bellingham Fire Department, 2006.
- Network Modeling uses interconnected linear features and point nodes to analyze how resources travel through networks. The linear features, like streets or river channels, have attributes that might define travel speed, number of lanes, and volume of flow. Nodes also have attributes that might identify vehicular turns and the time or cost required for each turn. Resources like water or traffic are placed in the network and their movement modeled. This way, problems with the network load can be identified.
